Architecture Layers - Model

EpyNN was made modular and architecture layers may be added or modified easily by following a few rules.

Layer is the parent layer (epynn.commons.models.Layer) from which all other layers inherit.
Class definition for custom layers must inherit from Layer and comply with the method scheme shown for the Template layer (epynn.template.models.Template).

Base Layer

Source code in EpyNN/epynn/commons/models.py.

Within the EpyNN Model, any architecture layer may be called such as model.layers[i] with an explicit alias for model.embedding. Layer instance attributes described below can be inspected from model.layers[-1].p['W'] for instance, which would call the weight associated with the last layer of the Network, predictably a Dense layer. All layers must inherit from Base Layer.

class epynn.commons.models.Layer(se_hPars=None)[source]

Definition of a parent base layer prototype. Any given layer prototype inherits from this class and is defined with respect to a specific architecture (Dense, RNN, Convolution…). The parent base layer defines instance attributes common to any child layer prototype.

__init__(se_hPars=None)[source]

Initialize instance variable attributes.

Variables

d (dict[str, int]) – Layer dimensions containing scalar quantities such as the number of nodes, hidden units, filters or samples.
fs (dict[str, tuple[int]]) – Layer forward shapes for parameters, input, output and processing intermediates.
p (dict[str, numpy.ndarray]) – Layer weight and bias parameters. These are the trainable parameters.
fc (dict[str, numpy.ndarray]) – Layer forward cache related for input, output and processing intermediates.
bs (dict[str, tuple[int]]) – Layer backward shapes for gradients, input, output and processing intermediates.
g (dict[str, numpy.ndarray]) – Layer gradients used to update the trainable parameters.
bc (dict[str, numpy.ndarray]) – Layer backward cache for input, output and processing intermediates.
o (dict[str, int]) – Other scalar quantities that do not fit within the above-described attributes (rarely used).
activation (dict[str, str]) – Conveniency attribute containing names of activation gates and corresponding activation functions.
se_hPars (dict[str, str or int]) – Layer hyper-parameters.

update_shapes(cache, shapes)[source]

Update shapes from cache.

Parameters

cache (dict[str, numpy.ndarray]) – Cache from forward or backward propagation.
shapes (dict[str, tuple[int]]) – Corresponding shapes.

Template Layer

Source files in EpyNN/epynn/template/.

An architecture layer may be defined as a finite set of functions (1).

\[layer = \{ f_1,...,f_n | n \in \mathbb{N}^* \} \tag{1}\]

In Python, this translates into a class which contains class methods. When designing a custom layer or attempting to modify one natively provided with EpyNN, one should be careful to not deviate from the organization shown below.

To avoid having to re-code the whole thing, child layer classes must at least contain the methods shown below. If the method is not relevant to the layer, as exemplified below, the same method should simply be made dummy. See the EpyNN Model training algorithm for details about the training procedure.

Finally, EpyNN was written to prevent users from having hundreds of lines of code within a class definition, which may negatively impact the educational side for peoples less experienced in programming. As such, methods are natively wrappers of simple functions located within a small number of files in the layer’s directory. Note that custom layers or further development do not need to stick this rule.

class epynn.template.models.Template[source]

Bases: epynn.commons.models.Layer

Definition of a template layer prototype. This is a pass-through or inactive layer prototype which contains method definitions used for all active layers. For all layer prototypes, methods are wrappers of functions which contain the specific implementations.

__init__()[source]

Initialize instance variable attributes. Extended with super().__init__() which calls epynn.commons.models.Layer.__init__() defined in the parent class.

Variables: trainable (bool) – Whether layer’s parameters should be trainable.

Shapes

Template.compute_shapes(A)[source]
Is a wrapper for epynn.template.parameters.template_compute_shapes().

Parameters

A (numpy.ndarray) – Output of forward propagation from previous layer.
def template_compute_shapes(layer, A):
    """Compute forward shapes and dimensions from input for layer.
    """
    X = A    # Input of current layer

    layer.fs['X'] = X.shape    # (m, .. )

    layer.d['m'] = layer.fs['X'][0]          # Number of samples (m)
    layer.d['n'] = X.size // layer.d['m']    # Number of features (n)

    return None
Within a Template pass-through layer, shapes of interest include:

Input X of shape (m, …) with m equal to the number of samples. The number of input dimensions is unknown.

The number of features n per sample can still be determined formally: it is equal to the size of the input X divided by the number of samples m.

Initialize parameters

Template.initialize_parameters()[source]
Is a wrapper for epynn.template.parameters.template_initialize_parameters().
def template_initialize_parameters(layer):
    """Initialize parameters from shapes for layer.
    """
    # No parameters to initialize for Template layer

    return None
A pass-through layer is not a trainable layer. It has no trainable parameters such as weight W or bias b. Therefore, there are no parameters to initialize.

Forward

Template.forward(A)[source]
Is a wrapper for epynn.template.forward.template_forward().

Parameters

A (numpy.ndarray) – Output of forward propagation from previous layer.

Returns

Output of forward propagation for current layer.

Return type

numpy.ndarray
def template_forward(layer, A):
    """Forward propagate signal to next layer.
    """
    # (1) Initialize cache
    X = initialize_forward(layer, A)

    # (2) Pass forward
    A = layer.fc['A'] = X

    return A    # To next layer
The forward propagation function in a Template pass-through layer k includes:

(1): Input X in current layer k is equal to the output A of previous layer k-1.

(2): Output A of current layer k is equal to input X.

Note that:

A pass-through layer is, by definition, a layer that does nothing except forwarding the input from previous layer to next layer.

Mathematically, the forward propagation is a function which takes a matrix X of any dimension as input and returns another matrix A of any dimension as output, such as:

\[\begin{align} A = f(X) \end{align}\]

\[\begin{split}\begin{align} where~f~is~defined~as: & \\ f:\mathcal{M}_{m,d_1...d_n}(\mathbb{R}) & \to \mathcal{M}_{m,d_1...d_{n'}}(\mathbb{R}) \\ X & \to f(X) \\ with~n,~n' \in \mathbb{N}^* & \end{align}\end{split}\]

Backward

Template.backward(dX)[source]
Is a wrapper for epynn.template.backward.template_backward().

Parameters

dX (numpy.ndarray) – Output of backward propagation from next layer.

Returns

Output of backward propagation for current layer.

Return type

numpy.ndarray
def template_backward(layer, dX):
    """Backward propagate error gradients to previous layer.
    """
    # (1) Initialize cache
    dA = initialize_backward(layer, dX)

    # (2) Pass backward
    dX = layer.bc['dX'] = dA

    return dX    # To previous layer
The backward propagation function in a Template pass-through layer k includes:

(1): dA the gradient of the loss with respect to the output of forward propagation A for current layer k. It is equal to the gradient of the loss with respect to input of forward propagation for next layer k+1.

(2): The gradient of the loss dX with respect to the input of forward propagation X for current layer k is equal to dA.

Note that:

A pass-through layer is, as said above, a layer that does nothing except forwarding the input from previous layer to next layer. When speaking about backward propagation, the layer receives an input from the next layer which is sent backward to the previous layer.

Mathematically, the backward propagation is a function which takes a matrix dA of any dimension as input and returns another matrix dX of any dimension as output, such as:

\[\begin{align} \delta^{k} = \frac{\partial \mathcal{L}}{\partial X^{k}} = f(\frac{\partial \mathcal{L}}{\partial A^{k}}) \end{align}\]

\[\begin{split}\begin{align} where~f~is~defined~as: & \\ f:\mathcal{M}_{m,d_1...d_{n'}}(\mathbb{R}) & \to \mathcal{M}_{m,d_1...d_n}(\mathbb{R}) \\ X & \to f(X) \\ with~n',~n \in \mathbb{N}^* & \end{align}\end{split}\]

Note that:

The f() parameter dA is the partial derivative of the loss with respect to output A of layer k.

The output of f(dA) is the partial derivative of the loss with respect to the input X of layer k.

The shape of the output of forward propagation A is identical to the shape of the input of backward propagation dA.

The shape of the output of backward propagation dX is identical to the shape of the input of forward propagation X.

The expression partial derivative of the loss with respect to is equivalent to gradient of the loss with respect to.

Gradients

Template.compute_gradients()[source]
Is a wrapper for epynn.template.parameters.template_compute_gradients(). Dummy method, there are no gradients to compute in layer.
def template_compute_gradients(layer):
    """Compute gradients with respect to weight and bias for layer.
    """
    # No gradients to compute for Template layer

    return None
A pass-through layer is not a trainable layer. It has no trainable parameters such as weight W or bias b. Therefore, there are no parameters gradients to compute.

Update parameters

Template.update_parameters()[source]
Is a wrapper for epynn.template.parameters.template_update_parameters(). Dummy method, there are no parameters to update in layer.
def template_update_parameters(layer):
    """Update parameters from gradients for layer.
    """
    # No parameters to update for Template layer

    return None
A pass-through layer is not a trainable layer. It has no trainable parameters such as weight W or bias b. Therefore, there are no parameters to update.

Note that: For trainable layers, this function is always identical regardless of the layer architecture. Therefore, it is not explicitly documented in the corresponding documentation pages. See epynn.dense.parameters.dense_update_parameters() for an explicit example.

Layer Hyperparameters

epynn.settings.se_hPars

Hyperparameters dictionary settings.

Set hyperparameters for model and layer.

se_hPars = {
    # Schedule learning rate
    'learning_rate': 0.1,
    'schedule': 'steady',
    'decay_k': 0,
    'cycle_epochs': 0,
    'cycle_descent': 0,
    # Tune activation function
    'ELU_alpha': 1,
    'LRELU_alpha': 0.3,
    'softmax_temperature': 1,
}
"""Hyperparameters dictionary settings.

Set hyperparameters for model and layer.
"""

Schedule learning rate

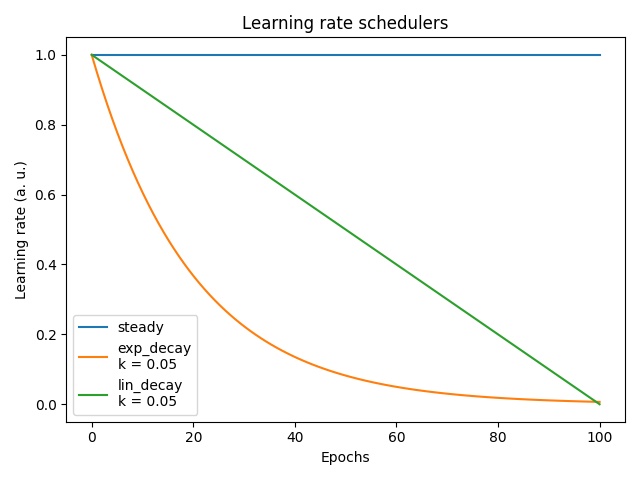
learning_rate: Greater values mean faster learning but at risk of the vanishing or exploding gradient problem and/or to be trapped in a local minima. If too low, the Network may never converge. Optimal values are usually in the - wide - range 1-10^-6 but it strongly depends on the network architecture and data.
schedule: Learning rate scheduler. See epynn.commons.schedule. Three schedulers are natively provided with EpyNN with corresponding schedules shown on the plot below. The principle of decay-based learning rate scheduling is to facilitate the Gradient Descent (GD) procedure to reach a minima by implementing fine tuning along with training epochs. It may also allow for greater initial learning rates to converge faster with a learning rate decay which may prevent the vanishing or exploding gradient problem.
decay_k: Simply the decay rate at which the learning rate decreases with respect to the decay function.
cycle_epochs: If willing to use cycling learning rate this represents the number of epochs per cycle. One schedule will basically repeat n times with respect to the total number of training epochs.
cycle_descent: If using cycling learning rate, the initial learning rate at the beginning of each new cycle is diminished by the descent coefficient.

Tune activation function

ELU_alpha: Coefficient used in the ELU activation function.
LRELU_alpha: Coefficient used in the Leky ReLU activation function.
softmax_temperature: Temperature factor for softmax activation function. When used in the output layer, higher values diminish confidence in the prediction, which may represent a benefit to prevent exploding or vanishing gradients or which will pictorially smooth the output probability distribution.